<封印吧,以神的名義! 創造多芒星封印術(一)>
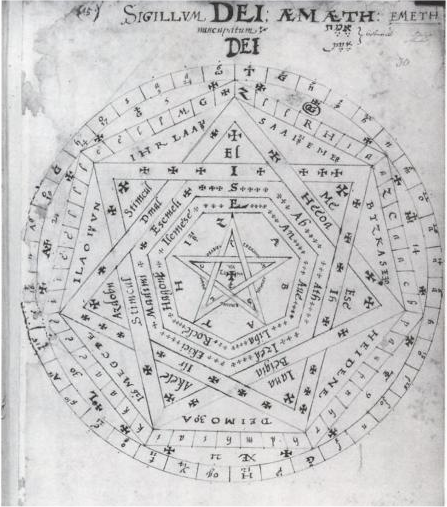 |
| Sigillum Dei 圖/Wikimedia Commons |
這樣的想法已擱置得積滿了塵,今天終於找了個擺放科普文章的角落,為各位獻上第一篇<封印吧,以神的名義! 創造多芒星封印術(一)>。
這個主題的產生源自於一次性質近乎是補救教學的教學實習,而那週的課程進度正是國中幾何(三角形、圓、角)。肉肉喵(筆者)思考了許久,有什麼旁門左道(亂用成語的邪門歪道)可以切入而不至於乏味,於是想起我家肉肉豬愛看動畫,而裡頭與幾何相關且最帥的莫過於主角開始封印時背景亮起的五芒星LED燈惹!!!((挨打
敲了訊息給肉肉豬問,哪幾部(年輕人看得)動畫裡頭有出現星形的,求救!無奈他在看海綿寶寶不理我...,而我只想到「重生吧,前鬼」女角召喚時會對著空氣畫五角星,原來已是20年前的動畫了,以及以色列的大衛星。
 |
| 不是我,是另個黃色的海綿。 圖/Wikimedia Commons |
 |
| 以色列國旗,上頭的六芒星即是大衛星。圖/Wikimedia Commons |
所以我說多芒星呢?
1. 畫出自己的五芒星
這個步驟可以找朋友一起,你可能會發現一些不同的畫法。
不會畫? 這兒有圖,描描也好...
 |
| 一個經典的五角星 圖/Wikimedia Commons |
2. 嘗試畫出七芒星
黑人問號.jpg
我知道,你說六芒星去哪兒了吧?不急,咱畫個七芒星先。
這兒會發現,有點難以直接繪出一顆七芒星,雖然七芒星不就是七個角的星形嗎,但是依照五芒星的畫法,似乎比較難去安排七芒星賦予角的順序。(繪製五芒星時,藉由轉折依序給出五芒星的各個角)
太小看你了,你還是畫出來了對吧,而他長這樣...
 |
| {7/2} 圖/Wikimedia Commons |
還是這樣呢?
 |
| {7/3} 圖/Wikimedia Commons |
於是乎,兩個長相迥異,但怎麼數都是七個角,而的確也都稱之為七芒星的圖案,在繪製過程中誕生。
怎麼辦,封印時畫錯可是會被怪物吃掉der。
 |
| OMG 要被吃掉惹 ㄉ 吶喊 圖/Wikimedia Commons |
分別以{7/2},{7/3}表示。
好似有次走進學生餐廳,直到餐點送上時才發現阿姨推薦的義大利麵根本就是奶油炒麵一般地錯愕與憤怒,不同的東西麻煩換個名字好嗎!(重點誤)
 |
| 中世紀末期魔法師John Dee的魔法陣(符),Seal of God 展於大英博物館。為{7/2}多芒星,亦為本篇名的命名來源。 |
當我們在嘗試繪製「多」芒星的同時,比起初期的「嘗試」,建構一種「方法」似乎更為恰當。
從「n」開始
當想要畫的角數越來越大,一個個畫,既容易錯亂,也難保不會有漏網之魚,於是我們回顧七芒星的繪製,過程中最常出現的困難是,角的擺放位置。因此,如果先固定住n芒星每個角的位置,那麼事情便好辦多了!
化圓囉((敲碗
回想劉徽割圓術的圖形,先畫一個圓,並再上頭平均地點上n個點,作為n芒星的n個角。接著,挑個起點,然後將七個點(角)以某種方法連線。
一般而言,我們會希望有某種規律的方式可以完成他,通常會是等間隔的畫法。例如把每個點依序標上數字1~n,等間隔畫法即是一組等差數列,如1,3,5,7,9...。
啊2,4,6,8...是不用畫逆?
這是個好問題,我們舉上圖{7/2}來當例子。
{7/2}只有七個角(廢話),所以我們依序會標上1,2,...,7。
如果採相同間隔的連線方式,直接連線倒是沒有問題,但若以數列寫下,便會發生有數字沒有得對應的情況,所以我們讓1,2,...,7每個數字都有除了自己以外的意義。例如,1代表1,同時也代表1+7或1+14也就是1+7*n,n為任意整數,同理,2代表2,也代表9,16,...,其餘數字以此類推。
將等差數列再次列出 1,3,5,7,9,11,13。
接著將超過7的數,以上面的方法替換,數列變成1,3,5,7,2,4,6。原本無以對應的2,4,6便成功回歸了。對照直接以間隔畫的圖形,順序一樣齁!這時可以發現,{7/2}中的2為間隔的意思。
動手做做看{7/3}。
然後你就可以畫出任意的芒星囉!!!
所有的芒星!!真的嗎!?
Q1. {m/n}中的m與n需要特別的條件嗎
Q2. 何以跳過六芒星
延伸閱讀 <封印吧,以神的名義! 創造多芒星封印術(二)>
從「n」開始
當想要畫的角數越來越大,一個個畫,既容易錯亂,也難保不會有漏網之魚,於是我們回顧七芒星的繪製,過程中最常出現的困難是,角的擺放位置。因此,如果先固定住n芒星每個角的位置,那麼事情便好辦多了!
化圓囉((敲碗
回想劉徽割圓術的圖形,先畫一個圓,並再上頭平均地點上n個點,作為n芒星的n個角。接著,挑個起點,然後將七個點(角)以某種方法連線。
啊2,4,6,8...是不用畫逆?
這是個好問題,我們舉上圖{7/2}來當例子。
{7/2}只有七個角(廢話),所以我們依序會標上1,2,...,7。
如果採相同間隔的連線方式,直接連線倒是沒有問題,但若以數列寫下,便會發生有數字沒有得對應的情況,所以我們讓1,2,...,7每個數字都有除了自己以外的意義。例如,1代表1,同時也代表1+7或1+14也就是1+7*n,n為任意整數,同理,2代表2,也代表9,16,...,其餘數字以此類推。
將等差數列再次列出 1,3,5,7,9,11,13。
接著將超過7的數,以上面的方法替換,數列變成1,3,5,7,2,4,6。原本無以對應的2,4,6便成功回歸了。對照直接以間隔畫的圖形,順序一樣齁!這時可以發現,{7/2}中的2為間隔的意思。
動手做做看{7/3}。
然後你就可以畫出任意的芒星囉!!!
所有的芒星!!真的嗎!?
假的。
 |
| 好喔。 |
Q2. 何以跳過六芒星
延伸閱讀 <封印吧,以神的名義! 創造多芒星封印術(二)>



留言
張貼留言